Chitarra Classica
Cav. Marco Sellitto
La chitarra classica, è prima
di tutto una cassa di risonanza che vibra: anche se il suo suono parte dalle
corde, quello che in realtà udiamo è il
suono della sua cassa armonica o cassa di risonanza che dir si voglia.
Più nel dettaglio :
Le corde, quando vengono pizzicate, determinano l’origine della vibrazione proprio come un oscillatore.
Il Ponticello, incollato sulla tavola armonica, riceve le vibrazioni delle corde, e attraverso la tavola armonica le trasferisce a tutta la cassa di risonanza del nostro strumento (quindi alle fasce laterali e, attraverso esse, al fondo).
Il ponticello è quindi l’elemento di accoppiamento tra questi due oscillatori: tavola armonica e corde.
La corda, essendo però molto sottile, sposta durante la sua vibrazione una quantità di aria così modesta che non sarebbe sufficiente a produrre un suono di sufficiente intensità…
Ed ecco che entra in gioco la cassa armonica dello strumento: la vibrazione generata dalla corda deve essere amplificata, arricchita di armonici, funzione per l’appunto demandata alla cassa di risonanza dello strumento , che sfrutta i due elementi di seguito indicati:
1) le caratteristiche vibrazionali della cassa armonica: in primis della tavola di risonanza (tavola armonica) e poi dei legni del resto della cassa (fondo e fasce)
2) il volume d’aria contenuto al suo interno: che “risuonando”, secondo la legge dell’oscillatore di Helmotz, amplifica in tal modo, il moto oscillatorio (vibrazione) delle corde
La vibrazione della cassa, infatti, mette in moto un gran volume d’aria sia all'interno della cassa di risonanza che intorno al suo corpo, producendo, in tal modo, la maggior parte del suono irradiato e quindi , quello percepito dall'ascoltatore e dal musicista stesso.
La tavola armonica della chitarra ha, in generale, un foro circolare sonoro (o, nel nostro caso , agli equivalenti, in termine di superficie , due fori semi circolari, ) che aumenta il livello di uscita (rinforzo), specialmente alle basse frequenze, proprio come una cassa acustica in bass-reflex,
e si ottengono i suoni degli strumenti che possiamo ascoltare anche in grandi sali da concerto.
Nello specifico, accade che Il legno, vibrando, sulla base del principio del risuonatore di Helmotz, mette in oscillazione l’aria circostante attraverso variazioni di pressione e questo accade sia per l’aria interna alla cassa sia per quella esterna.
Questo da origine a più modi di vibrazione dell’aria, la quale rinforza in particolar modo, le frequenze basse.
Quindi, oltre alla risonanza della cassa armonica, bisogna tener conto, nella costruzione di uno strumento, anche dei modi di vibrazione dell’aria. Questa, come qualsiasi materiale, è caratterizzata da particolari frequenze di risonanza, che sono legate direttamente: alle dimensioni, alla forma della cassa e del foro armonico, nonché alla sua rigidità strutturale e quindi alla sua facilità o meno di entrare in vibrazione.
Modello a tre masse di una cassa armonica di chitarra classica
Da un punto di vista acustico la chitarra classica, in termini di cassa armonica o di risonanza, è schematizzabile come un sistema vibrante costituito da 3 oscillatori[1]: Tavola armonica, fondo e la buca attraverso la quale l’aria con le sue risonanze (legge di Helmotz) entra ed esce dalla cassa, accoppiando tavola armonica e fondo.
Questo modello a tre masse è schematizzabile come segue:
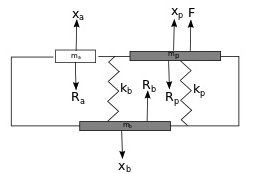
Fig. 1 modello a tre masse della cassa di risonanza di una chitarra classica
Dove:
Tavola armonica e fondo sono trattati come rigidi pistoni di massa rispettivamente mp e mb di effettive aree Ap e Ab rispettivamente.
1. mp è la massa della tavola armonica
2. mb è la massa del fondo
3. ma è la massa del foro (buca)
4. Xp il range (ampiezza) dello spostamento della tavola armonica (durante la vibrazione)
5. Xp il range (ampiezza) dello spostamento della tavola armonica (durante la vibrazione)
I prodotti:
1. Ap * xp = spostamento volumetrico tavola armonica
2. Ab * xb = spostamento volumetrico fondo
3. Aa * xa = spostamento del volume d’aria nella buca
Similmente le relative Ks rappresentano le rigidità dell’elemento strutturale e rappresentano perdite (compreso lo smorzamento delle radiazioni)Innovazioni progetto chitarra classica Cav Marco Sellitto
Premessa:
l’originale incatenatura Cav. Sellitto, nasce dalle seguenti osservazioni e considerazioni:
1. Qualsiasi raggiera, genera e delimita sempre e comunque, con la sua geometria, un preciso e definito campo di forze.
2. Area di tale campo di forze è la tavola armonica.
3. mediante l’implementazione dell’incatenatura si determina una “permanente “ accordatura della tavola armonica, che determinerà i modi di vibrazione della stessa e, di conseguenza, dell’intera cassa di risonanza.
4. nella storia passata e contemporanea della liuteria della chitarra classica, si è sempre frainteso lo scopo e quindi l’utilizzo delle catene della raggiera della tavola armonica, avendone una visione ridotta, esse sono state da tutti i liutai visualizzate ed utilizzate per la sola funzione di irrigidimento della struttura.
Invece esse hanno oltre a questa , un’altra funzione, che è paradossalmente , anche la più importante, che fino ad oggi , nessuno aveva identificato , e che viene invece utilizzata nel nuovo progetto di incatenatura della chitarra Cav. Sellitto :
Le catene della raggiera, sono come delle “vene del corpo umano”, che dovrebbero prendere il sangue (vibrazioni) dal cuore vibrazionale dello strumento, diffondendo tali vibrazioni in tutto il corpo (tavola armonica) e da essa a tutti gli elementi della cassa di risonanza ( fondo e fasce)…
Pertanto, oltre alla loro funzione di irrigidimento strutturale (unica funzione che ad oggi era stata identificata dai liutai di tutte le epoche), le catene della raggiera della tavola armonica, sono “in primis” dei dispensatori di energia vibrazionale dall’epicentro della vibrazione a tutte le arie vibrazionali dello strumento fino alle più periferiche.
La nostra nuova incatenatura sfrutta proprio questi nuovi principi:
La mia ricerca è partita quando ho cominciato ad indagare su quali potessero essere le vere cause della distorsione presente nel suono della chitarra.
Mi sono così reso conto che le cause della distorsione erano principalmente due: la posizione della buca di risonanza della tavola armonica e, ancora di più, la presenza delle due catene maestre della tavola armonica poste, usualmente, sopra e sotto la buca di risonanza.
Esse, per come sono strutturate, creano un forte irrigidimento localizzato in un’area che sarebbe invece deputata alla vibrazione.
Tutto questo genera delle disarmonie nella vibrazione della tavola, e di conseguenza, quei fenomeni di distorsione presenti nel suono della chitarra.
Ho così cominciato a pensare se c’era un modo per ridurre al minimo la distorsione o se non fosse addirittura stato possibile eliminarla del tutto.
Cominciandoci a studiare, mi sono reso conto che, per la posizione del foro armonico, la soluzione era già “ pronta sul tavolo” : Simplicio, infatti, già nel 1929 circa, aveva risolto questo problema spostando la buca in alto ai lati della tastiera.
Rimaneva però da risolvere la causa principale della distorsione del suono della chitarra classica, ossia la presenza delle due catene maestre della tavola armonica …
Partendo dal mio rifiuto dell’assioma secondo cui, per aumentare l’intensità del suono della chitarra, occorre agire sulla sua struttura con modifiche, tutte in qualche modo appartenenti alle categorie della “complicazione” e “dell’appesantimento”, la mia idea è infatti sempre stata quella che , per ottenere la massima prestazione sonora, occorresse procedere in senso opposto, quindi non aggiungendo, ma semplificando e togliendo tutto ciò che non era indispensabile alla stabilità dell’architettura, così, in quest’ottica, ho cercato una soluzione che mi consentisse di risolvere il problema alla radice : eliminare del tutto le catene maestre...
Fatti alcuni calcoli strutturali e relative simulazioni, sono riuscito a disegnare e poi realizzare una mia incatenatura che, non facesse uso delle due catene maestre.
Questo, senza in alcun modo sacrificare la stabilità strutturale della tavola armonica, che anzi ,da test di trazione e compressione su di essa condotti ,risulta essere addirittura più forte e stabile di quelle dotate di catene maestre.
Da un punto di vista acustico, la quantità di colori di suono che ne sono scaturiti è stato per me una enorme sorpresa che mi ha gratificato di tutti gli sforzi fatti…mi è sembrato di passare da un film bianco e nero ad uno finalmente… a colori…Partendo dallo studio delle risonanze dell’aria all’interno della cassa di risonanza: abbiamo riprogettato da un punto di vista strutturale, l’intera cassa di risonanza della chitarra classica, sfruttando i principi di acustica tali da operare in regime dinamico attraverso un continuo adattamento di impedenza acustica tra aria interna alla cassa di risonanza e l’aria esterna presente attorno alla cassa di risonanza, con cui come visto c’è scambio continuo. In particolare, in tal modo si è ottenuto, nel contempo un aumento dell’efficienza di un valore dell’ordine del +30% oltre che una riduzione della distorsione armonica.
La mia passione per l’opera di Tesla mi ha spinto a studiare un trattamento particolare del legno atto a creare una coesione molecolare tanto elevata , da rendere la tavola armonica tanto elastica, da riuscire a poter essere piegata a forma di U senza il rischio di romperla.
Si comincia con trattamenti termo-chimici a base di silicato di potassio, fino a
trattamenti con onde elettromagnetiche prima a bassa e poi ad alta frequenza che riescono a riorganizzare e orientare la struttura molecolare del legno, che grazie ai precedenti trattamenti, diventa più idonea ad essere “trattata”.
Con questo livello di flessibilità, le risposte della tavola ai modi vibratori delle corde risultano molto più sensibili e ampi, giungendo, in tal modo, ad un notevole arricchimento coloristico: è come offrire ad un pittore una tavolozza non soltanto più ampia, ma anche infinitamente più variata nelle tinte.
In tal modo, tra chi suona e il proprio strumento, si crea una sorta di “corto- circuito” in cui strumento e chitarrista diventano come un unico organismo vivente e creativo, così che l’offerta di nuovi colori induce l’interprete ad adeguare la propria “orchestrazione” all’ “organico” di cui dispone. In altre parole, si crea una sorta di feedback che trasforma anche l’esecutore.Ho così cercato di lavorare sull’elaborazione di una formula delle vernici, non già perché io pensassi che esse racchiudessero un mai svelato segreto del suono – come sostenevano alcuni mitografi dell’opera di Stradivari – ma perché ero certo di poter giungere ad un risultato che garantisse, insieme ai pregi già noti della verniciatura classica da liuteria (quella stesa a tampone, a base di spirito e gommalacca, per intenderci ), la riduzione ai minimi livelli dell’invasività della vernice sul suono dello strumento.
La fortuna di aver potuto lavorare su strumenti originali della scuola Cremonese ( Stradivari, Amati) come su alcuni Guadagnini, mi ha dato la possibilità di studiare quelle vernici e rendermi conto della loro poca invasività…
Ho così elaborato una mia procedura di verniciatura e finitura dello strumento, ad esse ispirate, che fa uso esclusivo di resine naturali, la cui formula ha messo a punto dopo aver lungamente studiato quelle della liuteria violinistica cremonese (dei grandi maestri : Amati, Guarneri e in particolar modo, Stradivari).
I miei strumenti montano corde progettate ad hoc, e di volta in volta personalizzate, che mettono in fase la loro tensione di precarico che eserciteranno costantemente sulla tavola armonica con valore del modulo di young della stessa tavola armonica dello strumento su cui esse verranno montate
A fine realizzazione di uno strumento è di fondamentale importanza “misurare” le performance acustiche raggiunte e misurare l’ eventuale scostamento che si è generato rispetto a quelle previste in fase di progetto.
QUALITÀ TONALE DELLA CHITARRA:
Nella valutazione musicale della qualità di uno strumento, si considerano principalmente tre caratteristiche: il volume sonoro, l’uguaglianza e il timbro in termini di ricchezza timbrica.
I. Il volume sonoro, grandezza che si può misurare facilmente quantitativamente, indica la “quantità di suono prodotta, quanto se ne propaga a una certa distanza e giunge alle orecchie dell’ascoltatore”, collocato a una certa distanza dalla sorgente sonora ( da vicino e da lontano per valutarne la proiezione) in grandi sale, e farsi sentire da un pubblico numeroso. Un fonometro, è lo strumento atto a misurare tale grandezza ed è oramai alla portata di tutti (oggi scaricabile anche con semplici app sui nostri smartpone)
II. L’uguaglianza o equilibrio, è “la capacità dell’istrumento di emettere suoni di intensità uniforme per tutte le note, a parità di forza impiegata nel pizzicare le corde”. È una caratteristica piuttosto rara: infatti quasi tutti gli strumenti a corde (sia chitarra classica, ma anche strumenti ad arco), presentano delle significative differenze in termini di intensità al variare dell’altezza delle note, spesso nel cambiare da una corda all’altra, o nel suonare la stessa nota su corde diverse. Queste differenze di volume fra una nota e l’altra, sono effetti che disturbano l’esecuzione di un brano, e sono dovuti principalmente a difetti nella distribuzione degli spessori nelle tavole.
III.
Il timbro è dato dalla sovrapposizione, diversa ad ogni
frequenza e per ogni strumento, della nota fondamentale e dei suoi armonici, in
altri termini la ricchezza armonica presente in un dato intervallo di frequenza
che si sta analizzando. Esso, è fortemente influenzato quindi dalla risposta in
frequenza dello strumento.
I test di Cimatica ci vengono, soprattutto per valutare quest’ultimo aspetto, ossia per la valutazione della qualità timbrica, oltre che per l’estensione in frequenza degli strumenti musicali oggetti del test.
Infatti, la ricerca ha dimostrato che le frequenze di risonanza delle modalità corporee degli strumenti non corrispondono a un valore grande o piccolo di efficienza radiazione acustica , è invece la forma modale che determina l'efficienza della radiazione. (Ian Perry “ Sound Radiation Measurements on guitars and other stringed musical instruments” Cardiff University UK). Ancora, i valori più significativi e su cui convergere lo studio dell’ efficienza di radiazione per le chitarre classiche si trvano tra 150 Hz e 450 Hz ((Ian Perry “ Sound Radiation Measurements on guitars and other stringed musical instruments” Cardiff University UK).
Perché l’analisi vibrazionale ? :
Il comportamento vibrazionale delle chitarre classiche, nonché dei violini , attraverso lo studio delle figure modali di Chladni è ben compreso. Sono stati fatti molti studi in tal senso soprattutto per la chitarra ( la relativa letteratura scentifica, in tale direzione, è estremamente ampia e completa).
Il suono emesso dalla chitarra classica, come visto, deriva da una componente vibrazionale e acustica assolutamente funzione coerente di quella vibrazionale: il comportamento vibrazionale infatti, descrive il trasferimento di energia dalle corde al corpo e i modi vibrazionali della cassa di risonanza della chitarra, che, con la loro vibrazione, generano il comportamento acustico, rappresentato dal suono irradiato dal movimento del corpo. Questo è il motivo, per il quale da decenni, le comunità scientifiche internazionali, trovano molto più rispondente a quanto riscontrato nella realtà, e in termini efficacia e completezza delle informazioni ricavate, studiare e analizzare , gli strumenti musicali ( a maggior ragione se di pregio come nel caso degli Stradivari, Amati, etc etc) attraverso lo studio delle figure di Chladni (cimatica), che con altre metodologie.
Mentre però grazie alla cimatica, il comportamento dei relativi strumenti è stato ampiamente descritto e approfondito, e su di esso come visto vi è ampia letteratura e documentazione scientifica, il comportamento acustico delle chitarre classiche , fino ad oggi, non era stato studiato nella stessa misura del comportamento vibrazionale .
Metodi di misurazione di Chladni:
Ciascuna parte del legno vibra con un’intensità diversa, e queste differenti intensità sono visualizzate dalle linee nodali e antinodali. Nodi e antinodi sono diversi a seconda della frequenza a cui vibra la tavola e per questo ciascuna risonanza è caratterizzata da una particolare configurazione nodale.
I modi vibrazionali generati a seguito delle varie frequenze sinusoidali forzatamente applicata alla tavola, sono funzione dell’incatentura (progetto) implementata su quella determinata tavola armonica.
Dalla CIMATICA (teorizzata da Hans Jenny) , e di cui il più grande precursore è stato Ernst Chladni, sappiamo che i corpi in vibrazione producono figure ad elevata forma simmetrica, tra le zone nodali ed antinodali di una superficie con specifica frequenza di risonanza: maggiore è il numero di figure modali, maggiore la simmetria delle figure generate e visualizzate sulla tavola armonica, tanto migliori saranno le prestazioni qualitative del relativo strumento.
Grazie all’ampia
sperimentazione condotta da vari studiosi e da varie università si scala
mondiale, nella correlazione tra il suono degli strumenti e le teorie cimatiche,
sappiamo che in termini qualitativi e quantitativi è possibile studiare in
maniera completa e affidabile, un violino o un qualsiasi strumento ad arco così
come anche una chitarra classica , generando e analizzando i modi vibrazionali,
che in seguito a frequenze sinusoidali
forzate, si generano sulla tavola armonica e che sono frutto dell’interazione
tra le tre masse vibrazionali principali (tavola armonica, fondo e vibrazione
dell’aria che accoppia, tavola armonica e fondo.
Se mettiamo della polvere di caffè, o materiale simile su un piatto vibrante, e forziamo su di esso una onda sinusoidale , a determinate frequenze, tale polvere assumerà ,delle forme particolari, dandoci la possibilità di verificare, quali e quanti sono i modi vibratori di una determinata tavola armonica, e della relativa cassa armonica, visualizzando delle vere e proprie figure.
Grazie all’osservazione e all’analisi morfologica delle figure nodali e antinodali che si visualizzano sulla tavola armonica.
Il numero di figure modali, e la loro simmetria sono direttamente proporzionali alla qualità vibrazionale e quindi acustica dello strumento in analisi.
Configurazioni di risonanza delle tavole armoniche
In che modo le proprietà meccaniche del legno sono legate alle risonanze di una tavola e, nel caso degli strumenti ad arco, a quali valori di queste grandezze fisiche corrispondono buoni risultati musicali del suono prodotto? I primi a studiare i modi di risonanza delle tavole di violini, con lo scopo di chiarire quali fossero queste relazioni, furono il fisico Felix Savart (1791-1841) e il liutaio Jean-Baptiste Vuillaume (1798-1875). A partire dal 1830 questi eseguirono esperimenti su una dozzina di violini costruiti da Antonio Stradivari e Giuseppe Guarnieri più di un secolo prima.
Dopo Vuillaume e Savart, il premio Nobel Chandrasekhara Venkata Raman (1888-1970), che per esempio fu il primo a spiegare esaurientemente un particolare fenomeno chiamato “nota del lupo”. Altri fisici e liutai da ricordare sono il fisico Frederick Saunders (1875-1963), e il liutaio Carleen Hutchins (1911-2009): Nel 1950 Carleen Hutchins, liutaio, e Frederik Saunders, fisico, iniziarono una serie di studi sulle risonanze delle tavole armoniche libere, cercando di spiegare in particolare in che modo queste fossero legate alle risonanze dell’intero strumento, oltre che alle sue caratteristiche timbriche. Per fare questo applicarono il metodo di Chladni, su circa 160 strumenti, sia antichi che costruiti apposta per gli esperimenti. Hutchins e Saunders, analizzando i vari modi di vibrazione di piano armonico e fondo e le frequenze alle quali i vari modi si presentavano.
La nostra tavola armonica risuona , a particolari frequenze, funzione : delle caratteristiche del legno, della incatenatura implementata, che accorda la tavola armonica in maniera permanente determinandone numero e modi vibrazionali.
Analizzando i risultati di più di 800 prove, arrivarono a confermare l’assoluta validità e completezza del metodo di Chladni per la determinazione della qualità di uno strumento musicale, che è diventato negli anni lo standard internazionale con cui studiosi e liutai, analizzano gli strumenti musicali.
Si mette in vibrazione la tavola mediante un altoparlante ad una specifica frequenza, e si osserva come si dispone della polvere di thè nero cosparsa sulla tavola armonica.
Cambiando la frequenza di tale vibrazione, si osserva a quale valore i granelli di polvere saltano di più: queste frequenze vengono definite come frequenze di risonanza della tavola.
I
granelli di polvere si dispongono seguendo delle precise geometrie fatte di
nodi e antinodi: chiaramente la polvere tenderà ad accumularsi nei punti nodali,
ovvero in quei punti in cui l’ampiezza dell’onda sonora è nulla. Mentre dove
l’ampiezza è massima o minima, gli antinodi, la polvere sarà fatta saltare via.
Analisi Modale :
Come per i violini, anche per la chitarra classica sappiamo che i modi vibrazionali, vale a dire le configurazioni morfologiche , che possono essere visualizzate ( o con tecniche indirette come laser, olografia, o dirette come la polvere da thè), sono 5 , classificati come modo di vibrazione
Abbiamo:
- modo 1 : presente in genere due volte : alla frequenza di Helmotz della nostra cassa armonica “A0” e a ca 185hz;
- modo 2 : presente alla frequenza di ca 285hz;
- modo 3 presente alla frequenza di ca 460 hz;
- modo 4 : presente alla frequenza di ca 510hz;
- modo 5 :presente alla frequenza di 645hz di seguito illustrati
Riportiamo di seguito alcune foto scattate sui modi visualizzati sulla chitarra Sellitto :
Alcuni esempi di MODO 1 (A0) , visualizzati :
Abbiamo risonanza del (modo 1 A0), già a 45hz, poi a 61hz,70 :
Osservazioni :
Dalle foto dei modi visualizzati
sulla tavola armonica, possiamo osservare:
1. Numerose frequenze a cui i modi principali si presentano ( es frequenza di risonanza di cassa: ricordando che il MI sesta corda a vuoto, con tuning 440 hz, corrisponde a ca 83hz, la nostra cassa ha risonanza fondamentale già a 45hz ( MODO 1- A0), ossia in termini di bassi è in grado di generare bassi a ca un ottava in più della nota più bassa della chitarra ( sesta corda. Vuoto), e, inoltre , presenta altri modi 1, rispettivamente 61hz e 70hz ).
Così come , presenta modo 5 ben 7 volte ,e più precisamente , alle seguenti frequenze : 587;613;650;890;1222;1362 fino alla frequenza di fino a 3132 hz ( considerando che , in termini di fondamentale , la nota più acuta della chitarra prima corda . XIX tasto) = 987 hz corrispondente al SI, i nostri 3132 hz corrispondono a ca due ottave più in alto) .
2. La perfetta simmetria delle figure visualizzate che ci testimoniano un fattore di qualità Q ideale.
3. Elevata estensione in frequenza ai bassi : 45hz ( che corrisponde al basso più profondo raggiungibile da un contrabbasso )
4. Elevata estensione in frequenza agli alti : 3132 hz ( che corrisponde alla massima frequenza acuta raggiungibile da un violino )
5. La costante presenza di risonanza a tutte le frequenze significative, evidenzia una risposta: ricca armonicamente, di alta intensità e assolutamente regolare ed uniforme.
Il carattere della chitarra ed il suo fattore di qualità è ben evidenziato ed influenzato dalla risposta in frequenza che essa presenta nel range di frequenze che vanno da ca 150hz a ca 450hz[1].
Abbiamo anche fatto una analisi spettrale di seguito, che testimonia la assoluta validità operativa del metodo cimatico, per l’analisi qualitativa, degli strumenti, per comodità di visualizzazione le abbiamo affiancate nello stesso grafico.
Per comodità abbiamo riportato gli uni affianco agli altri i grafici della risposta in frequenza delle chitarre 1-2-3-Sellitto nel range 150hz-450hz :
[1] Jurger Meyer “ acoustic and the performance of music—Classical Guitar” ; “Dynamic response optimization on an classical guitar” M.M.A.Von Boven.
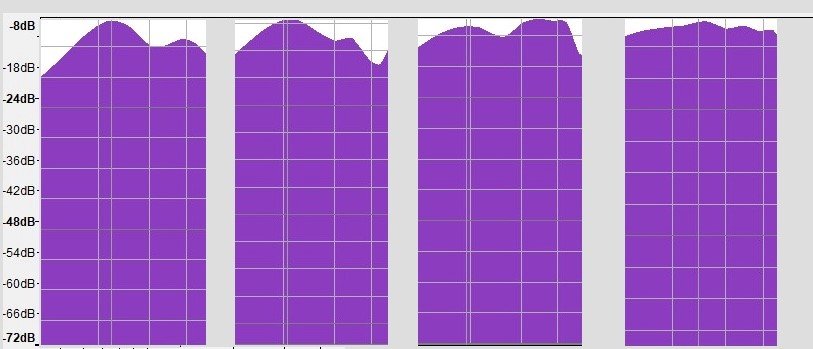
Analisi Spettrali (150hz-450hz)
a confronto, nell’ordine da sinistra verso destra :
chitarra 1( progetto
lattice brace)
chitarra 2 (progetto Double Top)
chitarra 3(progetto Hauser )
chitarra Cav. Sellitto (ultima a destra)
Notare che mentre le risposte
in frequenza di tutte le chitarre del test, sono assolutamente tormentante e irregolari,
la chitarra Sellitto, è quasi approssimabile ad una linea retta, ed è sempre
completamente “piena”, e quindi ricca di armoniche.
Questa risposta tanto ricca quanto lineare è dovuta
sia alla numerosità di frequenza a cui si presentano i modi di risonanza
fondamentali e sia all’elevata estensione della risposta in frequenza del
nostro strumento ( 45hz---3132hz), che “riempie” di componenti armoniche tutto
lo spettro armonico della chitarra.
Con questi ultimi test, abbiamo dimostrato anche l’ultimo punto, e vale a dire la assoluta ricchezza armonica e uniformità della risposta della chitarra Sellitto , rispetto a tutte le altre oggetto del test.
Conclusioni e punti di forza delle chitarre Cav Marco Sellitto:
Con le innovazione del progetto Cav Sellitto, la loro integrazione e , dopo i test finali a strumento costruito di messa a punto quello che si ottiene è :
Riduzione/eliminazioni dei punti di inerzia meccanica
Aumento dell'efficienza della tavola armonicae conseguentemente
Aumento dell'efficacia della radiazione definita come il rapporto tra la potenza acustica e la potenza meccanica immensa
Incremento dell’elasticità della tavola armonica, in grado di generare
più modi vibrazionali e a più frequenze
Incremento della risposta in frequenza delle alte frequenze della tavola armomica, in seguito all'incremento di forza e al contempo di elasticità della tavola armonica:
raggiungimento dei 3132Hz (massima frequenza alta di un violino)

riduzione di rigidità : raggiungimento dei 45hz a piena “ coppia di risonanza” (minima frequenza di un contrabbasso) :

11) Aumento della quantità di colori e sfumature timbriche della tavola
armonica
Di seguito riportate la risposta in frequenza , in termini di fondamentale , di alcuni strumenti :
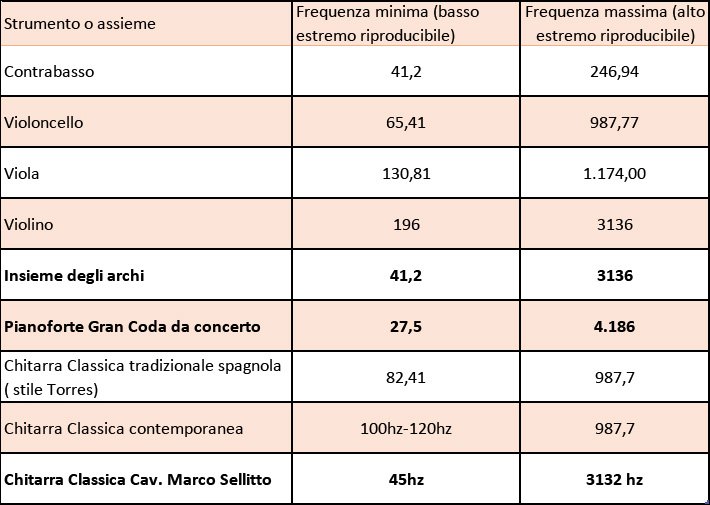
Tabella 1
Come si può notare dalla tabella sopra riportata , la chitarra realizzata secondo il nostro progetto, riesce a coprire una gamma di frequenze estesissima
Realizzando , concretamente , quell’idea di chitarra classica che il piu grande interprete della STORIA , il chitarrista Andrés Segovia definì come :
” una piccola orchestra “.








