Chitarra Classica
Cav. Marco Sellitto
クラシックギターという物は何より先ず振動する共鳴胴である。音は弦から発するが実際に我々の耳に届くのはボディ言い換えれば共鳴胴の音なのだ。
より詳細 :
弦ははじかれるとオシレーターのように振動を発生する。表面板に貼り付いたサドルは弦の振動を受け、表面板を通じギターのボディ全体(側面板から裏板まで)に伝える。
つまりサドルは表面板と弦というこの2つのオシレーターをつなぐ要素である。
しかしながら非常に細い弦は振動中極微量の空気しか動かせない為、充分強い音を発生させる事は出来ない…。
ここで共鳴胴の出番という訳だ。弦から発生した振動は調和豊かに増幅されなければならない。それがまさに共鳴胴に託された機能であり、以下2点の要素を利用する。
1) 共鳴胴の振動性特質 - 先ず表面板、次にボディの残り部分(裏板、側面板)の木材
2) 内部の空気量 - それは“ 共鳴しながら” ヘルムホルツ振動発生器の法則に従って弦の振動運動を増幅させる
ボディの振動は実際、共鳴胴内部とボディ周辺の多量の空気を動かし、よって聴衆と演奏者自身に聴き取られる大部分の放射音を発生させる。
一般的にギターの表面板には円形のサウンドホールが1つ(この場合もしくは表面に限り同等な小さ目のサウンドホールが2つ)あり出力レベルを上げ、特に低音をバスレフ型スピーカーの如く補強し、大きなコンサートホールでも聴こえるギター音が得られる。
具体的には、ヘルムホルツ共振器の原理に基づいて振動する木材が圧力変動によって周囲の空気を振動させる。この現象は、ボディ内部と外部の空気両方に起こる。 これにより空気の振動が起こり安くなり、特に低周波音が補強される。 ----------------------------------------
従って、楽器の構造ではボディの共鳴以外に空気の振動法も考慮する必要がある。 それは他のいかなる素材と同様、特定の共鳴周波数によって性質が決まる。それらの周波数は、ボディとサウンドホールの寸法・形状のみならず、構造上の硬度、つまり振動発生の容易さに直接関係する。
3質量型共鳴胴のクラシックギター
音響的観点からクラシックギターは共鳴胴の面で、3つの発振器から成る振動方式として図式化可能で ある[1]。表面板、裏板、そしてそれらを結合しヘルムホルツの法則に従い空気を共鳴させながら出入りさせるサウンドホールの3つだ。 この3質量型は次のように図式化出来る
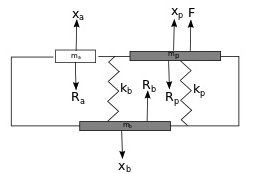
図1 3質量型共鳴胴のクラシックギター
表面板と裏板は各々有効面積Ap、Abの硬いピストン状の質量mpとmbで表す。
1 mp表面板の質量
2 mb裏板の質量
3. 3 maサウンドホールの質量
4 Xp (振動中)表面板の移動範囲(幅)
5. 5 Xp (振動中)表面板の移動範囲(幅)
乗法
1 Ap × xp = 表面板体積変位
Ab × xb = 裏板体積変位
Aa × xa =サウンドホール内空気体積変位
同様に、相対するKsは構造要素の硬さ、損失(放射減衰を含む)を表す。クラシックギター設計改革 カヴァリエーレ・マルコ・セッリット
前提
カヴァリエーレ・セッリット独自響棒は以下の観察と考慮から生まれる
1. 放線状構図は常にその形状によりはっきりと 正確な力場を限定しながら発生させる。
2.その力場面積を表面板とする。
3. 響棒の実装により表面板の“永続的” 調律が 定まり、それに伴い共鳴胴全体の振動の仕方も決定する。.
4. クラシックギター製作界において過去から 現代に渡り常に放射状響棒の目的と使用法は誤解 され続けて来た。視野の狭い全てのギター職人によって構造を硬化させる機能としてのみ見られて来た。
しかし響棒にはそれ以外にも、いやむしろ逆説的な最も大切な機能がある。それは今日まで誰にも発見されずカヴァリエーレ・セッリットのギターの響棒設計に初めて使用される。 :
放射状響棒は“人体の静脈”のようなものであり、ギターの心臓部、発振源から血液(振動)を得、全身(表面板)からボディの全要素(裏板、側面板)に至るまで 伝えるのだ。
つまり、表面板における放射状響棒は構造上硬化機能 (今日まであらゆる時代の弦楽器製作者によって承認されて来た唯一の機能)に加え、“何より”振動エネルギーを発生源地から周辺に至るまで全振動範囲に渡って分配する機能を果たす。
我々の新響棒は以下の原理を利用している。
私の研究はギター音に存在する歪みの真の原因は何かを調査する所から始まった。 こうして私は、歪みの原因は主に以下の2つだと気付いた。表面板のサウンドホールの位置と、又それ以上にサウンドホールの上下に平行し表面板内に設置される2本の主響棒の存在である。
それらは構造上、本来なら振動に委ねられる筈のエリアに極度の硬化を引き起こしてしまう。これら全ての 要因が表面板の振動に不調和を招き、その結果ギター音に存在するあの歪みの現象を引き起こす訳だ。
そこで歪みを最小限に抑える方法は無いか、いや むしろ完全に取り除いてしまう事は出来ないか と考え始めた。それに携わる研究を始めた時、サウンドホールの位置に関しての解決策は目の前にあった事に気付いた。シンプリシオは1929頃、ホールを上部指板寄りに移動させる事によって既にこの問題を解決していたのだ。
しかし、クラシックギターの音の歪みの主な要因である表面板の2本の主響棒の存在がまだ残った…。
ギターの音の強度を増すにはその構造自体にどうしても“複雑”で“ややこしく”なりがちな修正を施す必要がある、という自明の理に対する拒否感に基づく私の考えは以前から、音の効率を最大に高めるにはむしろ反対方向に向かうべき、つまり付加ではなく簡潔 化、更に建築上の安定性に不可欠でないのもの全てを 削除して行く必要があるというものだった。この視点から問題を根本的に解決する策を捜した結果、主響棒を完全に廃除してしまおうというという訳である…。
いくつかの構造上の計算と対策シミュレーションを行った後、2本の主響棒を使用しない独自の響棒のデザインとその作成に成功した。
これは勿論表面板の構造上安定性を決して犠牲にする事なく、むしろそれに対して行われた牽引及び圧縮実験から、主響棒を備えたものより強力で安定しているという結果が得られた。
音響の観点から、結果として生じた音の色彩の量は私にとって大きな驚きであり、全ての努力がむくわれ、白黒映画からようやくカラーになって行くようだったボディ内部の空気の共鳴を研究する事から出発した私達は、行き来し続ける共鳴胴内外の空気間に生じる音響インピーダンスへの持続的適応を通じ、動的体制で作用する程の音響原理を最大限に利用し、クラシックギターのボディを構造上観点から設計し直した。特にこの方法で機能効率が30%向上し、同時に調和の歪み削減も得られた。
テスラの業績に対する情熱から私は、木材の分子の凝集力を非常に高める事を目的とした特別な処理法で、割れる事なくU字型に折り曲がる程の弾力性を表面板に与える研究に没頭した。
それはケイ酸カリウムに基づく熱化学処理に始まり、先ず低周波、次に高周波で電磁波を処理する事によって木材の分子構造を再編成、及び配向する事を可能にする。こうした事前処理のおかげで木材は“扱われやすく”なるのだ。
このレベルの柔軟性により、弦の振動法に対する表面板の反応ははるかに敏感で幅広いものになり、著しく豊富な色彩効果に達する。
Iそれは画家に色の種類が豊富なだけでなく、色調が無限に変化するパレットを提供するようなもので、それにより演奏者と楽器の間に両者が一体化し生きた創造的有機体のようになる一種の“ショート”が生じる。 新たな色の提供により演奏者は自分に与えられた “組織”を合理的に活用しての“オーケストレーション”に適応するようになり、言い換えれば、演奏者も変えさせる一種のフィードバックが生じる訳である。クレモーナ地方弦楽器製作界(ストラディヴァリ、アマーティ) やグアダニーニの原作楽器を学べた幸運は、 彼等の塗料を研究しそれらの侵害性の低さを実感する機を与えてくれた。
こうして私は、ストラディヴァリをはじめ、 アマーティ、グアルネーリ等偉大な巨匠達によるクレモーナ地方ヴァイオリン製作技術に使われた樹脂を長期に渡って研究した結果、それらにイスピレーションを受け天然樹脂のみで調整する独自の塗料の処方を完成させるに至った。
楽器製作の最終段階で、達成された音響性能を “測定”し設計段階で予測されなかったずれが生じた場合、それを検証する事が基本的に重要である。
ギターの音質
楽器の品質を音楽的評価する際には、音量、均等性、音色の豊かさ、以上3つの特性が主に考慮される。.
1. 音量とは、容易に測定出来る大きさ、 発生される音の量を示し、ある一定の距離をおいてどれだけ広まり、且つ音の発生源から特定の距離(近距離、遠距離から検証)に位置する聴き手の耳にどれだけ大ホール内で届くか、多数の聴衆に聴こえるかを意味する。 騒音計とはその大きさを測定する器械の事で、今では誰でも手に入れる事ができる(スマートフォンのアプリダウンロード可) 。
2. 均等性又はバランスとは、 “同じ力で弦がはじかれた時全ての音符に対し均一の強度の音を出す楽器の能 力”の事である。これは比較的珍しい 特性で、実際ほぼ全ての弦楽器 (クラシックギターや擦弦楽器も含み)には音の高さを変えて行くにつれある弦から別のに変える時、もしくは同音符を 異る弦で弾く時、強度の点で大きな 違いが見られる事が多い。このような異る音符間の音量の差は曲の演奏に悪影響を及ぼし、それは主に板の厚さの配分上の欠陥により生じる。
3.音色とは、楽器ごと周波数ごとに変わる基音とその倍音の重なりの事で、言い換えると特定の周波数範囲内に存在する調和音の豊かさによって与えられる。従って音色は楽器の周波数応答に強い影響を受ける。サイマティクス検証は楽器の周波数拡張の他に何よりこの要素、音色の質を評価する為行なわれ る。
実際、研究により楽器の共振周波数は音響放射効率の高低に比例せず、放射効率は旋法形態によって決まる事がわかっている(イアン・ペリー“ギターほか弦楽器における音響放射測定”英カーディッフ 大学)。 更に、クラシックギターの放射効率の研究において焦点とされる最も重要な値は 150から450Hzとされる(イアン・ペリー“ギターほか弦楽器における音響放射測定” 英カーディッフ大学) 。
なぜ振動分析をするのか? :
Iクラドニ図形の研究を通しクラシックギター、ヴァイオリンの振動挙動はよく理解されている。何よりギターについては多数の研究がされている(それに関する科学文献は非常に豊富である) 。
クラシックギターが発する音は知っての通り、振動機能と完全に一貫する振動・音響的成分から生ずる。振動挙動とは実際、弦からボディに移動するエネルギーと共鳴胴の振動法を描写するものであ る。振動によりボディの動きから放射される音によって表現される音響挙動を発生させるのだ。これを根拠に数十年来国際的科学界で は、クラドニ図形を利用した楽器研究・分析(特にストラディヴァリウスやアマーティ等高級種)は他の方式より断然事実と相応し、そこから得られる情報は効果的で完成度が高いとみなされている。
このようにサイマティクスの功績によりそれに関する楽器の挙動は深く説明され科学文献も豊富だが、クラシックギターの音響挙動については今日まで振動挙動程は研究されていない。.
クラドニ図式
木の各部は異なる強度で振動し、これらの強度は節線と腹線によって視覚化される。節点と腹点は表面板が振動する周波数によって異なる為、各共振は特定の節点構成によりその性質が決まる。
I表面板に強制的に加えられる様々な正弦波周波数によって発する振動モードは、その特定の表面板に設置された響棒 (設計)の作用である。
エルンスト・クラドニを先駆者とするサイマティクス (ハンス・ジェンニーにより理論化された)により、 振動体は特定の共振周波数を与えた表面上での 節点領域と腹点領域間でほぼ対照的な形状を生成 する事がわかっている。表面板上にクラドニ図形が より対照的により多く生成され視覚化する程、その楽器の性能は高くなる。
世界規模で様々な学者や大学によって行われた広範囲な実験のおかげで、楽器の音とサイマティクス理論 の相関関係において、クラシックギターを含むヴァイオリン等のあらゆる弦楽器を完全且つ信頼性の高い方法でその音質、音量共を研究する事が可能とわかって いる。表面板に正弦波周波数が加えられ生成される振動モードは、3つの主要振動部(表面板、裏板と結合 する空気の振動、表面板と裏板)間での相互作用の産
物であり、その分析が行われる。
コーヒーパウダー等の粉を振動板に乗せある一定周波数で正弦波を強制的に加えてみると、粉は不思議な形状を帯びる幾何学模様を描き、それにより表面板と共鳴胴の振動モードの数と種を調べる事が出来る。
それは表面板に視覚化される節点と腹点の形態観測と分析の功績である。
I旋法形態の数とその対照性は分析される楽器の振動の質、つまり音響の質に直接比例する。
表面板の共振形成
木材の機械的特性はどのように表面板共振に関連するのか、また弦楽器ではこれらの物理量のどの値が生成される音の好結果に相当するのか。それらの関係を明らかにする事を目的としてヴァイオリン表面板の共鳴の仕方を最初に研究したのは、物理学者のフェリックス・サヴァート(1791~1841)と弦楽器製作者のジャン=バティスト・ヴィヨーム(1798~1875) だった。. 1830年以降、彼等はアントニオ・ストラディヴァリとジュゼッペ・グアルニエーリによって1世紀以上前に作られた多くのヴァイオリンで実験を行った。 ヴィヨームとサヴァートの後、例えばノーベル学者チャンドラシェカール・ヴェンカタ・ラーマン(1888~1970) が特殊な“ヴォルフ・トーン”と呼ばれる現象を 徹底的に解説した最初の人物となる。他に名を挙げておきたいのは物理学者フレデリック・サンダース(1875~1963)と弦楽器製作者カーリン・ハッチンス(1911~ 2009)である。1950年弦楽器製作者カーリン・ハッチンスと物理学者フレデリック・サンダースは表面板の共振について、特にそれがどのように楽器全体の共鳴及びその音色の特色と関係するのかを解明する為様々な研究を行なった。 彼等はこの研究の為に古い物、実験用に作られた物を合わせ約160台の楽器にクラドニ図形を利用した。両者は表面板、裏板の様々な振動モードとそれらが表れる周波数の分析を行った。
表面板は特定の周波数で、木材の特性と設置された響棒の機能によって共鳴する。これらの機能が表面板の振動数とモードを決定し、それを永続的に調律するのだ。.
800以上の検証結果の分析により、クラドニ図式における楽器の質測定の圧倒的有効性と完成度が認められ、後に学者や弦楽器製作者が楽器を分析するのに用いる国際的標準方法となった。
表面板にスピーカーにより特定の周波数で振動を与 え、表面板上にまかれた茶粉がどのように動くかを観察する。
周波数を変えながら、どの値で粉がより跳ねるか観察する。これらの値は共振周波数と定められる。
粉は節点と腹点で成る正確な幾何学模様に沿って並 ぶ。それは当然節点に、つまり音波の幅が無い所にたまって行き、幅が最大か最小の腹点では吹き跳ばされ る。
旋法分析 :
ヴァイオリンと同様にクラシックギターの場合も振動モード、つまり形態学的構成は視覚化可能であり(レーザーやホログラフィーのような間接的手法、又は茶粉等直接的手法により) 、そのモードは以下の5種類に 分類される事がわかっている。
- モード1 一般的に2度、ヘルムホルツ共鳴周波数 “A0” と、約185Hzで発生;
- モード2 周波数約285Hzで発生
- モード3 周波数約460Hzで発生
- モード4 周波数約510Hzで発生
- モード5 周波数約645Hzで発生
セッリット作ギターを使い振動モードを視覚化した写真を以下いくつか掲載しよう。
モード1(A0) 視覚化数例c , visualizzati :
モード1(A0)の共鳴が既に45Hzで、続き61、70Hzで見られる。
観測 :
表面板に視覚化された振動モードの写真から以下の事が観測される。
1. 主要振動モードは異なる多数の周波数で発生する。(例・共振周波数、チューニング440Hzの開放弦第6弦Eは約83Hzに相当する事から、我々の共鳴胴は 45Hz(モード1A0)で既に基本的共振を発生、つまり最低音(開放弦第6弦)より約1オクターブ高い所で低音を生成出来る。更に、61、70Hzで各々モード1が発生する)。 このように、モード5は7度、より正確には587、613、650、890、1222、 1362、3132Hzで発生、ここで言う 3132Hzは(基音で考えるギターの最高音は第1弦9フレットである事から)987HzでBに相応、つまり2オクターブ高い。 .
2.理想的品質係数を証明する視覚化された模様の完璧な対照性.
3.45Hzという低音周波数の顕著な拡張 (コントラバスの到達し得る最低音)
4.3132Hzという高音周波数の顕著な拡張 (ヴァイオリンの到達し得る最高音)
5.主要周波数全てに発生する持続的共振は調和的に豊かで強度が高く、完璧な規則性と均一性を持つ。
ギターの特性と品質の要素は約150から450Hzに及ぶ範囲の応答周波数に強調され影響される[注1]。.
又、楽器の上質な分析の為のサイマティクス手法の絶対的有効性を証明する以下のスペクトル分析も行い、わかりやすく同じグラフに並べてみた。
グラフは応答周波数範囲150から450Hzにおける ギター1、2、3とセッリット作の順である。
[1] Jurger Meyer “ acoustic and the performance of music—Classical Guitar” ; “Dynamic response optimization on an classical guitar” M.M.A.Von Boven.
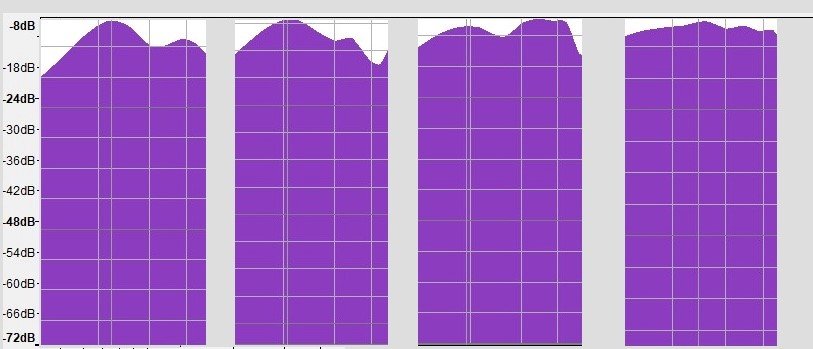
比較スペクトル分析(150~450Hz) 、左から順に
ギター1 (ラティスブレース設計)
ギター2 (ダブルトップ設計)
ギター3 (ハウザー設計) カヴァリエーレ
セッリット設計ギター(最後)
検証された全てのギターの応答周波数は完全に不規則なのに対し、セッリット作品のそれはほぼ直線に近く完全に“満杯” 、つまり倍音に豊富なのがわかる。.
この豊富で直線的な応答は、基本共振モードの発生する周波数が多数な事と、倍音スペクトルをその構成要素で満たす応答周波数の多大な拡張(150~450Hz)の両方が要因となっている。 以上の検証から最終論点も証明された。それは他のギターに比べセッリット作ギターは圧倒的に倍音が豊かで応答も均等している事である。
結論とカヴァリエーレ・セッリット作ギターの強み
カヴァリエーレ・セッリット設計のイノ ヴェーション導入・製作されたギターで行ったテストの結果、以下の点が検証される。
機械的惰性点の削減・廃除
その結果として表面板の性能の向上
音響の強さと莫大な機械的力間の比に定義される放線効率
表面板の弾力性向上により振動モードを複数の周波数でより多く生成可
表面板強度と弾力性の向上に伴う高周波での応答周波数の増加、3132Hz(ヴァイオリンの最大高周波) への到達
硬さ削減によるボディの主音低下に伴う低周波応答周波数の増加、最大“共振トルク” で45Hz (コントラバスの最小低周波)への到達
表面板の色調と音色ニュアンスの増加


11) 表面板の色調と音色ニュアンスの増加
表1
上の表からわかるように、私達の設計によって製作されたギターの周波数は非常に広範囲に及ぶ。
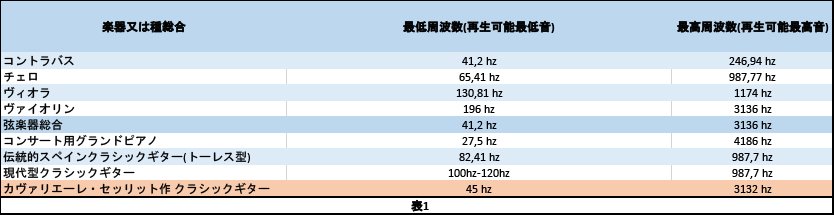
Tabella 1
Come si può notare dalla tabella sopra riportata , la chitarra realizzata secondo il nostro progetto, riesce a coprire una gamma di frequenze estesissima








